Also see in my zhihu(知乎) page with better reading experience: https://zhuanlan.zhihu.com/p/406628964

Foreword

这次的论文笔记的内容是CVPR’21的一篇论文“Understanding the Behaviour of Contrastive Loss”[1]。与以前看的很多讲模型这类论文不同，这篇paper没有模型，没有SOTA，而是对对比学习的loss中的temperature参数这个点进行深入剖析，更多的是偏数学理论的内容，并做实验进行验证，以此来达到题目所说的理解对比学习损失函数的目的。虽然知乎上已经有了这篇论文的笔记了，我还是决定自己写一遍，对论文的理解和印象可能更深刻一点。

Background

在写这篇论文笔记之前，我想先简单写一写对另一篇ICML’20的论文“Understanding Contrastive Representation Learning through Alignment and Uniformity on the Hypersphere”[2]的一点背景，因为CVPR这篇论文算是一定程度上Follow了他们的工作。

ICML这篇论文提出了两个对比学习的重要特性：Alignment和Uniformity. 定义如下：

Alignment: 对于Positive pair中的两个样本，应该被映射到相邻近的特征中。（即Encoder需要将相似的样本编码为相似的特征向量）

Uniformity：所有特征向量应该在超球面空间* (hypersphere) 中几乎均匀地分布，以保留数据中尽可能多的信息。（即特征分布需要最大化保留信息）

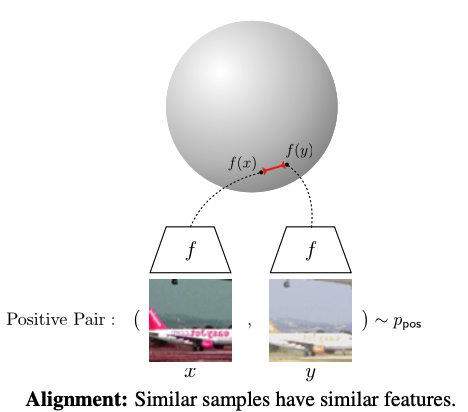
alignment
uniform

其实我认为这两个特性也自然地体现了对比学习的目的$s(f(x),f(x^+))>>s(f(x),f(x^-))$，即$x$和与其相似的正样本$x^+$在$f(\cdot)$编码后的相似度$s(\cdot)$，应该远大于$x$和与其不相似的负样本$x^-$编码后的相似度。而这两个特性，从对比学习的loss也能窥知一二。
$$
\mathcal{L}(x_i)=-\log[\frac{\exp(s_{i,i}/\tau)}{\sum_{k\neq i}\exp(s_{i,k}/\tau)+\exp(s_{i,i}/\tau)}]\ \ \ \ \ \ \ \ \ \ (1)
$$
其中$s_{i,j}=f(x_i)^Tf(x_j)$ 。

可以简单地将二者的公式写成如下形式[3]：(这公式看着简单，要用LaTex打出来可学到好几个命令\underset, \mathop, \limits, \rm什么的)

eq2

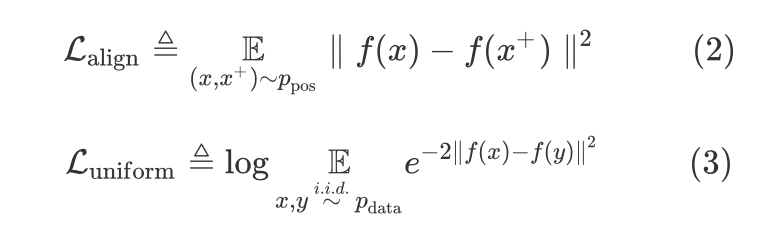
其中，$\mathcal{p}{ pos}$ 为positive pair的分布，$\mathcal{p}{data}$ 为data distribution，即样本数据分布。

作者通过实验验证了这两个特性与模型性能的关系，即通过以上公式计算出的Alignment和Uniformity两种度量值越小，encoder能够得到更好的表示，模型表现越好（Acc越高）。即下图中越蓝的点，准确率越高，且集中在左下角，两个度量值都很小的地方。

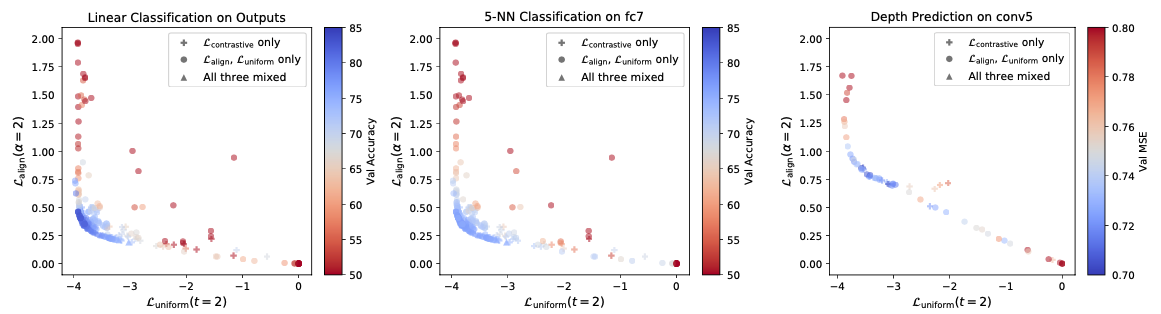
align-unif-plot

Alignment和Uniform度量值与模型Performance的关系

这两个metric代码也非常简单，作者直接贴到了论文里。

# bsz : batch size (number of positive pairs)
# d : latent dim
# x : Tensor, shape=[bsz, d]
# 	latents for one side of positive pairs
# y : Tensor, shape=[bsz, d]
# 	latents for the other side of positive pairs
def align_loss(x, y, alpha=2):
    return (x - y).norm(p=2, dim=1).pow(alpha).mean()

def uniform_loss(x, t=2):
    return torch.pdist(x, p=2).pow(2).mul(-t).exp().mean().log()

接下来我们回到最初的CVPR这篇论文。

Introduction

我认为这篇论文就是上一篇的一个递进，其一个核心思想就是引入样本之间潜在的语义结构的概念：模型得到的特征表示过于均匀（uniformity）的话，会不能很好地容忍语义相似的样本（语义相似的样本表示分离较远），从而破坏了这种样本之间潜在的语义结构，影响下游任务的表现。①从这一个idea出发，作者将这种现象定义为一种uniformity-tolerance的两难困境（我们既希望特征表示足够均匀地分布使其便于分割开，又希望其能容忍语义结构相似的样本）；$\rightarrow$ ②而为什么会出现这种现象，作者用对比学习loss中的参数temperature $\tau$ 作为切入点，探讨了其是如何影响embedding的分布；$\rightarrow$ ③而如何影响这种分布是因为temperature的大小控制使得contrastive loss有一种hardness-aware的特性，即temperature越小，对那些更难的负样本的Gradient梯度更大，使得这些样本的特征表示更加分离，从而得到的整体的特征分布更加均匀。这里的更难的负样本，是指那些与锚点anchor $x$ 很相似/属于同一类的样本（对于$x$而言，其增强的样本$x^+$才是正样本，其余都叫做负样本），所以对于encoder来说，要区分开他们的表示会更难。

虽然我觉得好像我复述的这一段故事好像也说得通，但是这篇论文实际上的结构好像跟我的思路是相反的。作者是③先提出contrastive loss的hardness-aware特性，$\rightarrow$②再提出这种特性是temperature这个参数导致和控制的，$\rightarrow$①最后提出temperature与uniformity之间的关系，并以此定义uniformity-tolerance dilemma这个现象。

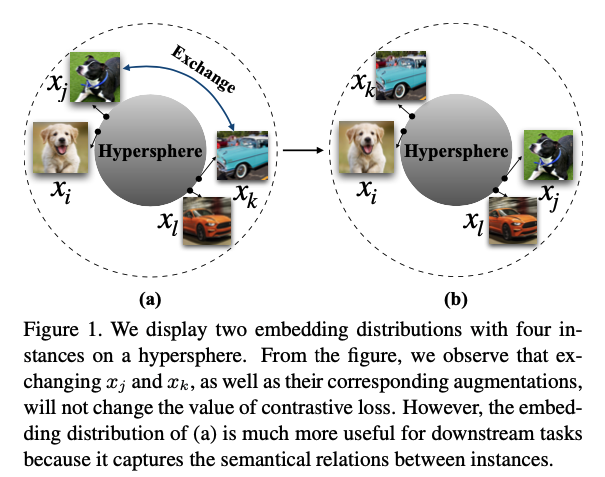
为了更好地理解作者提出的语义结构的影响，作者用下图作解释。对于(a)(b)两种embedding分布而言，我们将$x_j$与$x_k$的embedding交换，并不会改变其对比学习的loss，但是，(a)的这种分布将$x_i,x_j$两个都是“狗”的样本表示集中在一起，$x_l,x_k$两个都是“车”的样本表示集中在一起，比(b)这种分布在下游任务中表现更好，因为它能够体现出样本间潜在的语义结构。我觉得这个图很有意思，当时还以为作者下面要讲怎么在hypershere上通过不停地交换来使得同类样本更近了（大雾）。现在回过头来看，其实这个图也一定程度上体现出uniformity-tolerance的关系，即这个图代表着一种理想情况：当uniformity保持不变时，特征表示却能够更加体现出语义结构（更能容忍语义结构相似的样本）。这也是作者后面做实验想要达到的一个效果。

exchange

那temperature是不是真的会影响embedding的分布呢（②）作者用T-SNE可视化了$ \tau=0.07$ 和$\tau=0.2$ 两种情况下的embedding分布。可以看到$ \tau=0.07$ 时分布更加均匀（uniform），而$\tau=0.2$ 时分布更加局部集中-全局分离（即相似/同类的样本更集中，不相似/不同类的样本相隔更远）。也就是从这里，作者提出uniformity-tolerance困境的（①）。

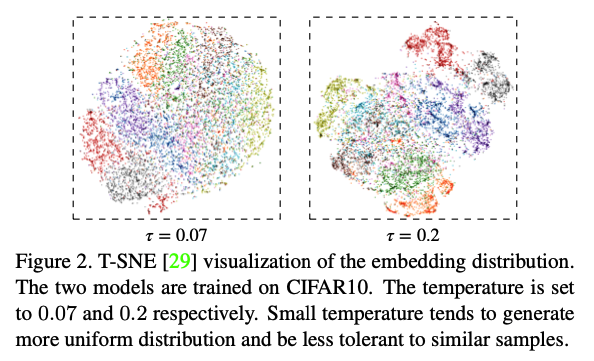
Hardness-aware Property③

作者在对比学习原始loss，即Eq.(1)的基础上，提出一个简单形式的loss，也可以满足拉近positive pair和分隔negative samples的目的：
$$
\mathcal{L}_{\rm simple}(x_i)=-s_{i,i}+\lambda\sum\limits_{i\neq j}s_{i,j} \ \ \ \ \ \ \ \ \ \ (4)
$$
作者将Eq.(1)的原始loss对正例相似度$s_{i,i}$和负例相似度$s_{i,j}(j\neq i)$求导，得到以下两个式子：
$$
\frac{\partial\mathcal{L}(x_i)}{\partial s_{i,i}}=-\frac{1}{\tau}\sum\limits_{k\neq i}P_{i,k} \ \ \ \ \ \ \ \ (5)
$$

$$
\frac{\partial\mathcal{L}(x_i)}{\partial s_{i,j}}=\frac{1}{\tau}P_{i,j} \ \ \ \ \ \ \ \ (6)
$$

其中
$$
P_{i,j}=\frac{\exp(s_{i,j}/\tau)}{\sum_{k\neq i}\exp(s_{i,k}/\tau)+\exp(s_{i,i}/\tau)} \ \ \ \ \ \ \ \ (7)
$$
通过(6)作者发现对于不同的negative sample $s_{i,j}$ ，其梯度是与(7)中的分子$\exp(s_{i,j}/\tau)$成比例的（对于样本$i$的所有负样本$j$而言，$P_{i,j}$的分子不同，分母相同），不同的$s_{i,j}$的梯度不同（$s_{i,j}$越大，梯度越大；$\tau$越小，则越放大了这个梯度），因此体现出其Hardness-aware的特性。这个特性与简单化的loss Eq.(4)不同，$\mathcal{L}{\rm simple}$对$s_{i,j}$求导后只是固定的值$\lambda$。

观察(5)式，其实$P_{i,k}$与(6)式的$P_{i,j}$是一样的（$j$和$k$都只是表示一个不同于$i$的样本，二者可以互换），两个梯度的绝对值之比$(\sum_{k\neq i}|\frac{\partial\mathcal{L}(x_i)}{\partial s_{i,k}}|)/ |\frac{\partial\mathcal{L}(x_i)}{\partial s_{i,i}}|=1$ ，即，$|\frac{\partial\mathcal{L}(x_i)}{\partial s_{i,j}}|/ |\frac{\partial\mathcal{L}(x_i)}{\partial s_{i,i}}|$是满足概率分布的，其和为1。令$r_i(s_{i,j})=|\frac{\partial\mathcal{L}(x_i)}{\partial s_{i,j}}|/ |\frac{\partial\mathcal{L}(x_i)}{\partial s_{i,i}}|$ 来表示对于负样本$x_j$ 的相对梯度。
$$
r_i(s_{i,j})=\frac{\exp(s_{i,j}/\tau)}{\sum_{k\neq i}\exp(s_{i,k}/\tau)}, i\neq j \ \ \ \ \ \ \ (8)
$$
根据Eq.(8)，作者画出了不同的$\tau$值下$r_{i,j}$关于$s_{i,j}$的分布，如下图。横坐标为$s_{i,j}$，纵坐标为$r_{i,j}$，不同颜色的线代表不同的$\tau$ 值。可以发现，当temperature $\tau$ 越小（蓝色线），$s_{i,j}$相似度越大时，$r_{i,j}$ 陡增；而$s_{i,j}$相似度很小时，曲线趋于均匀平滑。也就是说，对于与$x_i$ 越相近的负样本$x_j$，loss对其”惩罚”就越大（梯度越大）。当$\tau$非常小时，会导致对比loss只集中火力在离$x_i$最近的那一两个样本上，试图将他们分隔开②。

r_s

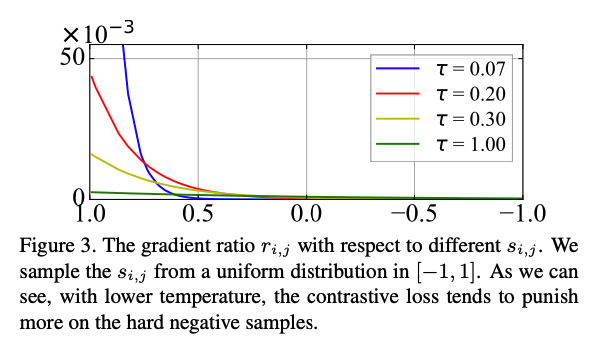
Uniformity-Tolerance Dilemma①

作者分别用两小节介绍了Uniformity和Tolerance两个属性，并绘制了在不同数据集下，不同temperature与两个属性值的关系。由于Uniformity在Background那节里介绍过了，这里主要介绍一下Tolerance的定义和计算方式。

Tolernace: 指对于属于同一类的样本他们的平均相似度，表示语义相关的样本的分布集中程度。

$$
T=\underset{x,y\sim p_{\rm data}}{\mathbb E}[(f(x)^Tf(y))\cdot I_{l(x)=l(y)}] \ \ \ \ \ \ \ \ (9)
$$

其中，$l(x)$表示$x$的类别，$I_{l(x)=l(y)}$是一个指示函数（indicator function），当$l(x)=l(y)$时，其值为1；当$l(x)\neq l(y)$时，其值为0。

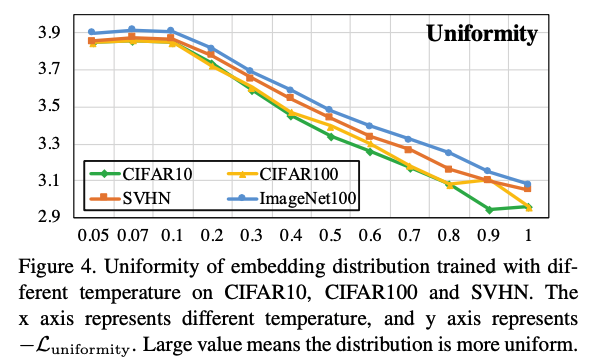
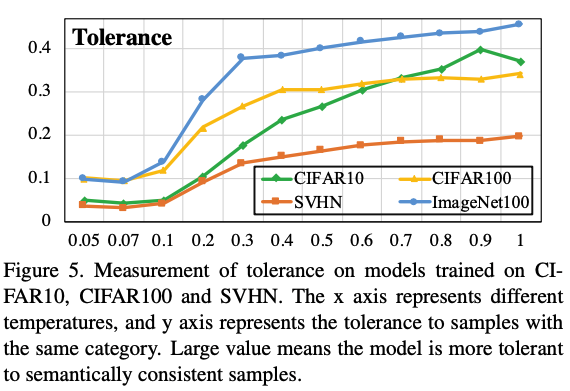
uni_temp tol_temp

Figure 4表示了不同的temperature（横轴）在不同的数据集上对 $-\mathcal{L}{Uniformity}$ 的度量值大小（纵轴），随着temperature的增大，$-\mathcal{L}{Uniformity}$ 在减小，也就是 $\mathcal{L}_{Uniformity}$ 在增大，根据其计算方式，说明embedding的分布变得更不均匀了。而对于Figure 5则可以看到，随着temperatrue的增大，tolerance这个值也在增大，说明语义相关的样本的相似度在变大。一个理想的模型，应该是局部聚集，全局均匀的，也就是tolerance要大的同时，uniformity要小。但根据上面两个图，tolerance增大时，uniformity也在增大；tolerance减小时，uniformity也在减小，这便形成了一个作者所定义的Uniformity-Tolerance Dilemma。所以对于一般的对比学习loss而言，如何选择一个合适的temporature来平衡embedding的聚集性和均匀性，是需要根据具体问题来权衡的。

我觉得这个思想可以说是一定程度上继承了Background那节里的ICML那篇论文的思想，那里的Alignment和这里的Tolerance很像，但是，也正如我在Introduction开头所写的，这篇论文主要就是引入了样本之间语义结构的概念。Alignment只是考虑了Positive pair的聚集程度，而这篇论文进一步，考虑了同一类相似样本的聚集程度。

Breaking Point

作者利用了之前的一篇研究工作中提出的Hard contrastive loss策略 [4]，在计算对负样本的梯度时，只截取相似度大于某个阈值的负样本计算（如选取Top K最近的负样本）。这样的话，相当于放大了负样本的作用，使得当temperature变大时，模型最后形成的embedding分布会更均匀一点，而不会像Figure 4 那样随着temperature增大embedding分布变得更不均匀。以此缓解Uniformity-Tolerance Dilemma中调节temperature对uniformity变化的影响。也呼应了Figure 1中“当uniformity保持不变时，特征表示却能够更加体现出语义结构“的目的。

Hard Contrastive Loss定义如下：
$$
\mathcal{L}{\rm hard}=-\log \frac{\exp(s{i,i}/\tau)}{\sum_{s_{i,k}\geq s^{(i)}\alpha}\exp(s{i,k}/\tau)+\exp(s_{i,i}/\tau)} \ \ \ \ \ \ \ \ (10)
$$
其中，$s^{(i)}_\alpha$ 是负样本与anchor $x_i$ 的一个相似度分界点，对于相似度在 $[s^{(i)}\alpha,1.0]$ 这个区间（informative interval）的负样本被看作是informative hard negative samples（与anchor更相似，更难将他们分隔开），而对于相似度在 $[-1.0,s^{(i)}\alpha]$ 这个区间，则被称作uninformative interval。在计算loss时 $s_{i,j}<s^{(i)}_\alpha$ 的这些负样本，使其$r_i(s_{i,j})=0$。相当于将原本负样本的梯度比例分布（如Figure 3）压缩到informative interval的这个区间，从而增强模型对在该区间内负样本的“惩罚”，集中火力把与 $x_i$ 相似的负样本推远。

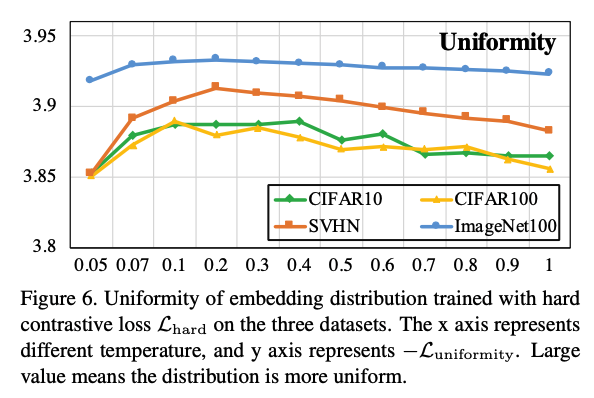
采用$\mathcal{L}_{\rm hard}$ 得到的不同数据集下，不同temperature与Uniformity和Tolerance两个属性值的关系图如下。将Figure 6和Figure 4相比可以发现，此时随着temperature增大，Uniformity保持较稳定不变。此时增大temperature便可以在保持uniformity不增大的情况下，增大Tolerance，即模型得到的embedding既保持均匀，又能局部聚集，从而保留一定潜在语义结构，破解上一节所说的Uniformity-Tolerance Dilemma问题。

hard-1 hard_2

Conclusion

在本篇论文中，作者从temperature这个参数入手，从理论和实验的角度指出Contrastive Loss是一个hardness-aware的损失函数，而temperature在控制embedding分布中扮演着重要作用，并由此提出一种Uniformity-Tolerance Dilemma问题。针对这个问题，未来还有待研究。

* 注1: 超球面空间hypersphere: 当所有类别的样本很好地各自聚集在一起并在空间中形成一个球面时，他们是线性可分的。而这一特性是欧几里得空间做不到的。如下图，用一个线性分类器，可以找到一个角度切割球面将“猫”这一类的样本与其他样本分隔开。

hypersphere